вправа 3.11 гдз 11 клас математика (геометрія) Нелін Долгова 2019
Вправа 3.11
Умова:
Знайдіть площу бічної поверхні правильної трикутної призми, площа основи якої дорівнює S, а площа перерізу, проведеного через сторону однієї основи й протилежну вершину іншої основи, дорівнює Q.
Розв'язання:
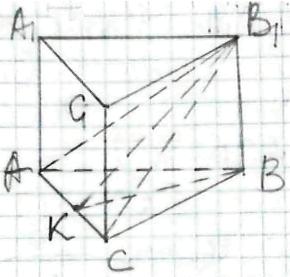
АВСА1В1С1 - правильна призма,
ВВ1 ┴ (АВС),
ВВ1 - висота призми.
ΔАВС - рівносторонній,
SΔАВС = S,
ΔАСВ1 - переріз, проведений через сторону АС і вершину В1.
SΔАВ1С = Q - площа перетину.
Знайдемо Sбіч. - площу бічної поверхні призми.
Нехай а = АВ = АС = ВС -
сторона основи, тоді \begin{equation} a=\sqrt{\frac{45}{\sqrt{3}}} \end{equation} ΔАВС - ортогональна проекція ΔАВ1С.
Нехай φ - кут між площинами
(АВС) і (АВ1С), тоді \begin{equation} cos\varphi =\frac{S}{Q} \end{equation} Із ΔАВС: (ВК - висота ΔАВС) \begin{equation} BK=\frac{2S}{a}= \end{equation} \begin{equation} =\frac{2S}{\sqrt{\frac{4S}{\sqrt{3}}}}=\sqrt{S\sqrt{3}} \end{equation} З формули \begin{equation} tg^{2}\alpha+1=\frac{1}{cos^{2}\alpha }, \end{equation} маємо \begin{equation} tg\alpha =\sqrt{\frac{1}{cos^{2}\alpha }-1} \end{equation} Тоді \begin{equation} tg\varphi =\sqrt{\frac{1}{cos^{2}\varphi }-1} \end{equation} \begin{equation} tg\varphi =\sqrt{\frac{1}{(\frac{S}{Q})^{2}}-1}= \end{equation} \begin{equation} =\sqrt{\frac{Q^{2}}{S^{2}}-1}= \end{equation} \begin{equation} =\sqrt{\frac{Q^{2}-S^{2}}{S}} \end{equation} Із ΔВКВ1 (ВК - висота ΔАВС,
В1К - висота ΔАВ1С),
∠В1ВК - 90°.
ВВ1 = ВКtgφ \begin{equation} BB_{1}=\sqrt{\frac{Q^{2}-S^{2}}{S}}\cdot \end{equation} \begin{equation} \cdot \sqrt{S\sqrt{3}}= \end{equation} \begin{equation} =\frac{1}{S}\sqrt{S\sqrt{3}(Q^{2}-S^{2})}. \end{equation} Площа бічної поверхні призми:
Sбіч. = Росн. • ВВ1 =
= 3а • ВВ1 = \begin{equation} =3\cdot \sqrt{\frac{4S}{\sqrt{3}}}\cdot \frac{1}{S} \end{equation} \begin{equation} \sqrt{S\sqrt{3}(Q^{2}-S^{2})}= \end{equation} \begin{equation} =\sqrt{\frac{6}{S}}\sqrt{\frac{S^{2}}{\sqrt{3}}\cdot \sqrt{3}(Q^{2}-S^{2})}= \end{equation} \begin{equation} =\frac{6S}{S}\sqrt{Q^{2}-S^{2}}= \end{equation} \begin{equation} =6\sqrt{Q^{2}-S^{2}}. \end{equation}
